|
Black/Scholes-Formel
Black/Scholes formula. Mathematische Formel zur Bewertung von Optionen in stetiger Zeit. Die B. /S.-F. wurde Anfang der 70er Jahre von Black, Scholes und Merton als erste geschlossene Lösung zur Bewertung von europäischen Optionen (European Option) auf Aktien ohne Berücksichtigung von Dividendenzahlungen und auf Aktienindizes entwickelt. Der Formel liegt die Überlegung zugrunde, dass auf vollkommenen und arbitragefreien Märkten aus einer Aktie und leerverkauften Optionen (Leerverkauf) auf die Aktie ein im Zeitablauf risikoloses Portefeuille gebildet werden kann (dynamische Hedgingstrategie). Ein solches Portefeuille muss mit dem risikolosen Zinssatz bewertet werden, so dass der Optionspreis die einzig unbekannte Größe im Bewertungsproblem ist. - Der Herleitung liegen folgende Annahmen zugrunde: 1. Die Aktienkurse folgen einem Random Walk (Random-Walk-Theory) in Form einer geometrischen Brownschen Bewegung. - 2. Alle Investoren sind risikoavers und maximieren den Nutzen des Endvermögens. - 3. Die Bewertung der Assets erfolgt anhand homogener Erwartungen (vollkommener Kapitalmarkt). - 4. Der Kapitalmarkt ist vollkommen. - 5. Alle Investoren haben unbeschränkten Zugang zum Kreditmarkt, an dem sie zum einheitlichen risikolosen Zinssatz Kapital anlegen und aufnehmen können (Wiederanlageprämisse). - Die B./S.-F. für den Fair Value einer europäischen Call-Option C lautet: 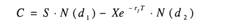 Anhand der Put-Call-Parity ergibt sich der Fair Value für eine europäische Put- Option P als: Anhand der Put-Call-Parity ergibt sich der Fair Value für eine europäische Put- Option P als: 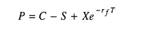
<< vorhergehender Fachbegriff |
|
nächster Fachbegriff >> |
|
|
|
|
